Predictive Analytics in Tableau Part 9: Automatic Time Series Analysis

Today, we will talk about automatically performing time series analysis using Tableau 8.1's new R functionality.  Up to now, we've looked at ways to determine which type of exponential or ARIMA model fits the data best.  However, the number of models can be overwhelming to an analyst with less statistical exposure.  Today, we'll look at how to let R choose the model for you.  As usual, we will use the Superstore Sales sample data set in Tableau.

Let's imagine that we came up with a candidate list of models and want to see which ones are better for our type of data.

Too Many models

Here, we can see that charts can easily get very messy to see which models are best when there are a lot of models.  So, what better way is there?  Now, we're going to introduce two functions that will help.  The function ets() will create an appropriate Exponential model for your data and auto.arima() will create an appropriate ARIMA model for your data.  Like always, the code is identical until the last couple of lines.  You can find the full code in the appendix at the end of this post.  Here are the last couple of lines:

Exponential Model

fit <- ets(timeser)

c(rep(NA, len.new), forecast(fit)[[4]][1:hold.orig])

ARIMA Model

fit <- auto.arima(timeser)
(rep(NA, len.new), forecast(fit)[[4]][1:hold.orig])

Now, let's look at our chart.

Automatic Models

As you can see, these calculations quickly gave us two "good" candidate models to look at.  You might notice that neither of these models fits the data extremely well.  However, we could look at these models and see that the ARIMA model doesn't seem to be able to account for any of the variability, which is a very bad thing.  The Exponential model seems much better, but still needs some tweaking.  Therefore, we could throw out all of the ARIMA models and focus on creating a better Exponential model.  In just a couple of minutes, we were able to narrow our modeling down to a single family!  That's a huge time saver.  Perhaps we could even improve this process by adding new functions and new techniques.  But, that's a topic for another post.  Thanks for reading.  We hope you found this informative.

Brad Llewellyn
Data Analytics Consultant
Mariner, LLC
llewellyn.wb@gmail.com
https://www.linkedin.com/in/bradllewellyn

Appendix

ARIMA (Auto)

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- auto.arima(timeser)
    c(rep(NA, len.new), forecast(fit)[[4]][1:hold.orig])
",


ATTR( MONTH( [Order Date] ) ), ATTR( YEAR( [Order Date] ) ), SUM( [Sales] ), [Months to Forecast] )

Exponential (Auto)

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- ets(timeser)
    c(rep(NA, len.new), forecast(fit)[[4]][1:hold.orig])
",


ATTR( MONTH( [Order Date] ) ), ATTR( YEAR( [Order Date] ) ), SUM( [Sales] ), [Months to Forecast] )

Predictive Analytics in Tableau Part 8: ARIMA Time Series

Today, we will talk about creating ARIMA time series models using Tableau 8.1's new R functionality.  In layman's terms, an ARIMA model uses three different numeric parameters to make varying types of time series models.  The ARIMA family is one of the most researched and respected families in the field of Time Series Analysis.  It is also used by a number of automated prediction tools like SQL Server Analysis Services.  As usual, we will use the Superstore Sales sample data set from Tableau.

The most important part of creating an ARIMA model is choosing the parameters.  The parameters are as follows:

AR  - Autoregressive
I      - Integrated
MA - Moving Average

We won't delve heavily into what each of these parameters does.  However, we will talk about methods for selecting them.  First, let's take a look at our data.

Sales by Month

Now, let's look at choosing the AR parameter.  In order to do this, we need to look at the Partial Autocorrelation Function (PACF).  Just like with the previous posts, almost all of the code is used to create the time series.  Only the last line is used to give us the PACF values.  The full code can be found in the appendix at the end of the post.

rep(pacf(timeser, plot=FALSE)$acf,5)[1:len.orig]

Now, let's look at these values.

Sales by Month (PACF)

The question we want to ask is "Starting at the beginning, how many consecutive values are above .25 or below -.25?"  We can easily accomplish this with colors.

AR Colors

Sales by Month (PACF with Color)

We can see that there are no values above .25 or below -.25.  So, there doesn't seem to be an AR component to this model.  Next, let's move on to the MA component using a very similar technique.  Moving Average components can be analyzed using the Autocorrelation Function (ACF).  Here's the last line of code.

rep(acf(timeser, plot=FALSE)$acf,5)[1:len.orig]

Now, let's look at the values.

Sales by Month (ACF with Color)

The first value is always guaranteed to be 1 and should be ignored.  We see that the values after one aren't really worth noting.  Therefore, the MA component in the model is 0 and the AR component is 0.  Now, let's look at the Integrated portion of the model.  R has a nice built-in function called ndiffs() that tells us what the I component should be.  Here's the last line of code.

ndiffs(timeser)

Now, let's see the value.

Sales by Month (I Component)

Here, we see that our I component should be zero.  This leaves us with a bit of an interesting conundrum.  An ARIMA(0,0,0) model is basically useless.  It is guaranteed always return the mean (average) value.  So, this means that the ARIMA family is not a good fit for this data.  Just for kicks, let's swap this data out for another data set that does fall in the ARIMA family.  So, let's look at a data set with monthly Unemployment values for the US.

Unemployment by Month

Now, let's look at the ARIMA components.

Unemployment by Month (ARIMA Components)

We can see that there are 3 consecutive AR values above .25 or below -.25, and I of 0, and 2 MA values (the first of which we ignore).  So, our model should be ARIMA(3,0,1).  Now, let's see what our forecasts look like.

Unemployment by Month (Forecast)

We can see that the ARIMA model seems to be pretty good at predicting the up-and-down motion of the data.  However, the recent rise in unemployment has caused some variability that the model doesn't handle very well.  Fortunately, there are plenty of other families of models out there.  Thanks for reading.  We hope you found this informative.

Brad Llewellyn
Data Analytics Consultant
Mariner, LLC
llewellyn.wb@gmail.com
https://www.linkedin.com/in/bradllewellyn

EDIT: An anonymous user noted an error in the original appendix.  The R variables were defined as 

year.orig <- .arg1
month.orig <- .arg2

while our assignment at the end of the segment was defining

ATTR( MONTH( [Order Date] ) ) = .arg1
ATTR( YEAR( [Order Date] ) ) = .arg2

This has now been fixed an all of the code should be valid.  Many thanks to our readers for pointing that out.

Appendix

AR Component

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg2
    month.orig <- .arg1
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    rep(pacf(timeser, plot=FALSE)$acf,5)[1:len.orig]
",

ATTR( MONTH( [Order Date] ) ), ATTR( YEAR( [Order Date] ) ), SUM( [Sales] ), [Months to Forecast] )

I Component

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg2
    month.orig <- .arg1
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    ndiffs(timeser)
",

ATTR( MONTH( [Order Date] ) ), ATTR( YEAR( [Order Date] ) ), SUM( [Sales] ), [Months to Forecast] )

MA Component

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg2
    month.orig <- .arg1
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    rep(acf(timeser, plot=FALSE)$acf,5)[1:len.orig]
",

ATTR( MONTH( [Order Date] ) ), ATTR( YEAR( [Order Date] ) ), SUM( [Sales] ), [Months to Forecast] )

Forecast (ARIMA(0,0,1))

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg2
    month.orig <- .arg1
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- arima(timeser, order=c(0, 0, 0))
    c(rep(NA, len.new), forecast(fit)[[4]][1:hold.orig])
",

ATTR( MONTH( [Order Date] ) ), ATTR( YEAR( [Order Date] ) ), SUM( [Sales] ), [Months to Forecast] )

Forecast (ARIMA(3,0,1))

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg2
    month.orig <- .arg1
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- arima(timeser, order=c(3, 0, 1))
    c(rep(NA, len.new), forecast(fit)[[4]][1:hold.orig])
",

ATTR( MONTH( [Order Date] ) ), ATTR( YEAR( [Order Date] ) ), SUM( [Sales] ), [Months to Forecast] )

Predictive Analytics in Tableau Part 7: Double and Triple Exponential Time Series

Today, we will talk about creating Double and Triple Exponential Time Series using Tableau 8.1's new R functionality.  If you read our previous post, Single Exponential Time Series, you remember that we were only able to predict a constant value for all future observations.  Trend and Seasonality were not considered using the Single Exponential.  These models should fix all of that.  Once again, we will use the Superstore Sales sample data set from Tableau.

At its core, a single exponential time series can predict values without trend (increase or decrease over longer periods of time) or seasonality (repetition of patterns at regular intervals, i.e. yearly, monthly, etc.).  The double exponential time series adds trend to the model while the triple exponential time series adds trend and seasonality.  We're also adding the model that accounts for seasonality without accounting for trend.  We're not sure what this model is called, so we'll call it the Reverse Double Exponential Model for now.  If you have any idea what it's called or if it's invalid for some reason, please let us know in the comments.  The code is almost identical like before, just with the second to last line changed.  You can find the full code in the appendix at the end of this post.

Double Exponential

fit <- HoltWinters(timeser, gamma=FALSE)

Reverse Double Exponential

fit <- HoltWinters(timeser, beta=FALSE)

Triple Exponential

fit <- HoltWinters(timeser)

Now, let's look at these predictions.

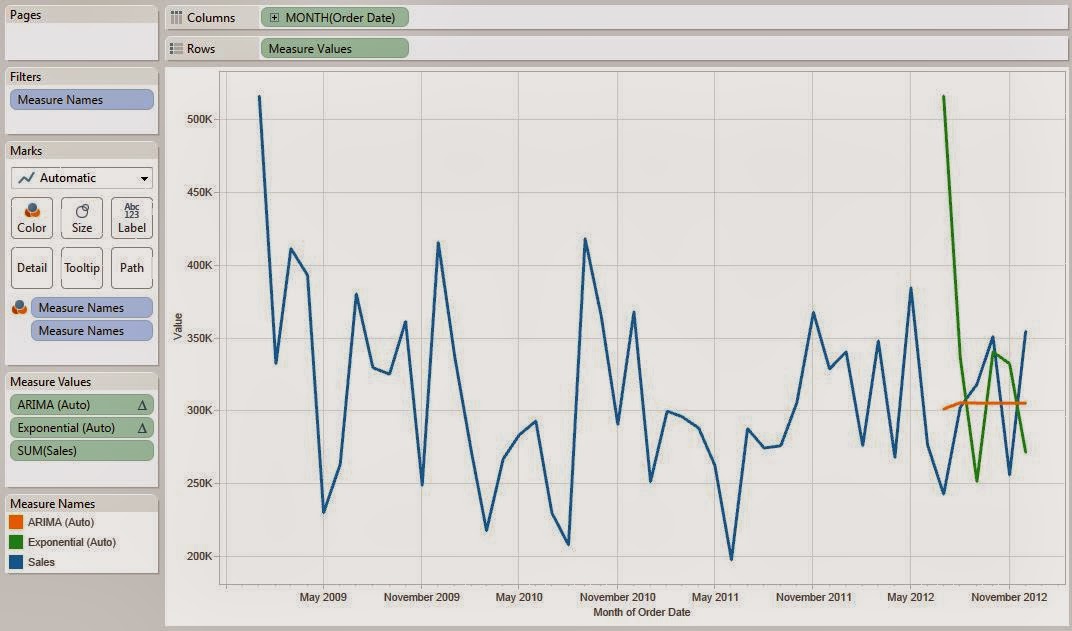
Sales by Month (Predictions)

We can see that the green line (Double Exponential) is straight.  This is exactly what we expected.  However, there is some definite seasonality in this data that we need to account for.  The orange line (Triple Exponential) seems to follow that seasonality, but the trend seems to have pushed it too high.  The red line (Reverse Double Exponential) appears to be the "Goldilocks" model.  It accounts for the seasonality, but doesn't let the trend drag it too high.  For further examination, let's look at the 95% confidence intervals for these models to see which models fit the data more tightly.

Sales by Month (Bounds)

We can easily see that the green bounds (Double Exponential) are so spread out that they become basically worthless.  Also, the orange bounds (Triple Exponential) and the red bounds (Reverse Double Exponential) seem to the same except that the orange bounds are shifted up slightly higher, which is exactly what we saw with the predictions as well.  Therefore, we have good evidence to say that the Reverse Double Exponential model is the best fit for this data.  Now, let's use the same trick as last week to predict new values by adding blank rows to our data set.

Sales by Month (Reverse Double Exponential with Bounds)

Now, we have seemingly accurate predictions using a well-respected time series model.  However, we're not done with this yet.  There are other families of time series models we could use.  There's also artificial neural networks, naive bayes, and much more.  Thanks for reading.  We hope you found this informative.

Brad Llewellyn
Data Analytics Consultant
Mariner, LLC
llewellyn.wb@gmail.com
https://www.linkedin.com/in/bradllewellyn

Appendix

Double Exponential

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, gamma=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$mean)
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),
 [Months to Forecast] )

Double Exponential (Lower 95%)

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, gamma=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$lower[,2])
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),

 [Months to Forecast] )

Double Exponential (Upper 95%)

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, gamma=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$upper[,2])
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),

 [Months to Forecast] )

Reverse Double Exponential

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, beta=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$mean)
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),
 [Months to Forecast] )

Reverse Double Exponential (Lower 95%)

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, beta=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$lower[,2])
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),

 [Months to Forecast] )

Reverse Double Exponential (Upper 95%)

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, beta=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$upper[,2])
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),

 [Months to Forecast] )

Triple Exponential

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$mean)
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),

 [Months to Forecast] )

Triple Exponential (Lower 95%)

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$lower[,2])
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),

 [Months to Forecast] )

Triple Exponential (Upper 95%)

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$upper[,2])
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),

 [Months to Forecast] )

Predictive Analytics in Tableau Part 6: Single Exponential Time Series

Before we start today's topic, we want to direct you towards a great source of information about Tableau 8.1's R functionality.  This page was compiled by members of the Tableau community and can be found here.  Now, on to the demonstration.

Today, we will talk about creating time series analyses using Tableau 8.1's new R functionality.  In our previous demonstrations, we used varying regression techniques to predict values.  These techniques took into account the relationships between the variables, but not across time.  Time Series Analyses approach from the opposite direction.  They attempt to predict new values by looking at previous (or future) values in time, but only considering one variable.  For this demonstration, we will use the Superstore Sales sample data set from Tableau.

As always, the first step is to look at the data we want to forecast.  Let's look at Total Sales per Month.

Sales by Month

We can see that there is quite a bit of variation in this data.  Now, we run into our first conundrum.  I don't know of an easy way to allow Tableau to see dates outside of what's in the data.  Therefore, we can only forecast for dates we already have in the data.  This is actually a good and bad thing for us, as we'll soon see.  If you have a system that includes budget data for the future, then the dates will already be available and you won't have this problem.  Alas, we do not have such luck.  So, let's first hold out the last six months of our data and create the model using only data up to June 2012.  That way, we have something to compare our forecasts to.  In order to do this, we create an integer parameter.

Months to Forecast

Now, we can dynamically set the number of months we want to forecast.  Next, we need to create the code to do this.  But, before we do that, we need to install the "forecast" package on the R Server.

Install Packages

If you don't have the access to do this, then you will probably need to talk to the administrator on your R server.  Fortunately, we host the server on our local machine; so, there is no issue.  Now, back to the forecasting.

This code is long and somewhat complex.  So, we'll only touch on the important parts.  The code for Sales (Forecast) is as follows:

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1],
                     dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, beta=FALSE, gamma=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$mean)
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),
 [Months to Forecast] )

First, we need to install the forecast library using library(forecast).  Then, we need to sort the data by date, and hold out the last few months.  How many months get held out depends on the value of our [Months to Forecast] parameter.  Finally, we fit our time series as a single exponential model and output the results.  Let's see what it looks like.

Sales by Month (with Forecast)

As you can see, the forecast is pretty close to the true values.  This type of model cannot pick up on the trend or seasonality though.  We'll deal with that in a later post.  For now, let's see how well this model fits by also plotting the 80% and 95% confidence intervals.  You should remember confidence intervals from our posts about regression.  The code for the intervals are identical to the code for the forecast, with the exception of the last line of code.  I'll post the final lines here.  If you want to see the full code, please refer to the appendix at the end of this post.

Sales (Forecast) (Lower 80%)

c(rep(NA,len.new), forecast(fit, hold.orig[1])$lower[,1])

Sales (Forecast) (Lower 95%)

c(rep(NA,len.new), forecast(fit, hold.orig[1])$lower[,2])

Sales (Forecast) (Upper 80%)

c(rep(NA,len.new), forecast(fit, hold.orig[1])$upper[,1])

Sales (Forecast) (Upper 95%)

c(rep(NA,len.new), forecast(fit, hold.orig[1])$upper[,2])

Now, let's see what the intervals look like

Sales by Month (with Forecast and Bounds)

We can see that all of the actual values fall well within the 95% bound.  This means that our model fits our data reasonably well.  Now, let's talk about how to use this model to predict future values.  The simplest way we could find to do this is to add some filler lines to your data set.  In our case, we're using an Excel spreadsheet.  So, we add the following lines to our data.

Adding Empty Dates

You should note that if you are doing forecasts for a specific type of product, customer, etc., you will need to duplicate these dates for every combination of dimensions you want to forecast over.  Now, when we refresh our worksheet, we have our forecasts.

Sales by Month (with Future Forecast and Bounds)

One very important thing to notice about these forecasts is that the bounds are extremely far from the graph.  This would seem to imply that the model is not a good fit for the data.  Therefore, we would want to use a different type of time series model for it.  Unfortunately, that's going to have to wait until the next post.  Thanks for reading.  We hope you found this informative.

P.S.

If anybody can think of a better way to get future forecasts for dates that don't exist in the data, please let us know in the comments.  Also, this method is not robust against missing data.  If you're data has some missing months/week/etc., you may have to alter the method slightly.

Brad Llewellyn
Data Analytics Consultant
Mariner, LLC
llewellyn.wb@gmail.com
https://www.linkedin.com/in/bradllewellyn

APPENDIX:

The code for Sales (Forecast) (Lower 80%) is as follows:

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, beta=FALSE, gamma=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$lower[,1])
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),
 [Months to Forecast] )

The code for Sales (Forecast) (Lower 95%) is as follows:

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, beta=FALSE, gamma=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$lower[,2])
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),

 [Months to Forecast] )

The code for Sales (Forecast) (Upper 80%) is as follows:

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, beta=FALSE, gamma=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$upper[,1])
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),

 [Months to Forecast] )

The code for Sales (Forecast) (Upper 95%) is as follows:

SCRIPT_REAL("
    library(forecast)

    ## Creating vectors

    hold.orig <- .arg4
    len.orig <- length( hold.orig )
    len.new <- len.orig - hold.orig[1]

    year.orig <- .arg1
    month.orig <- .arg2
    sales.orig <- .arg3

    ## Sorting the Data

    date.orig <- year.orig + month.orig / 12
    dat.orig <- cbind(year.orig, month.orig, sales.orig)[sort(date.orig, index.return = TRUE)$ix,]
    dat.new <- dat.orig[1:len.new,]

    ## Fitting the Time Series

    timeser <- ts(dat.new[,3], start = c(dat.new[1,1], dat.new[1,2]), end = c(dat.new[len.new,1], dat.new[len.new,2]), frequency = 12)
    fit <- HoltWinters(timeser, beta=FALSE, gamma=FALSE)
    c(rep(NA,len.new), forecast(fit, hold.orig[1])$upper[,2])
"
, ATTR( YEAR( [Order Date] ) ), ATTR( MONTH( [Order Date] ) ), SUM( [Sales] ),

 [Months to Forecast] )