Azure Databricks: Delta Lake, Part 1

Today, we're going to talk about Delta Lake in Azure Databricks.  If you haven't read the previous posts in this series, Introduction, Cluser Creation, Notebooks, Databricks File System (DBFS), Hive (SQL) Database and RDDs, Data Frames and Dataset (Part 1, Part 2, Part 3, Part 4), they may provide some useful context.  You can find the files from this post in our GitHub Repository.  Let's move on to the core of this post, Delta Lake.

Per Azure Databricks documentation, "Delta Lake is an open source storage layer that brings reliability to data lakes. Delta Lake provides ACID transactions, scalable metadata handling, and unifies streaming and batch data processing. Delta Lake runs on top of your existing data lake and is fully compatible with Apache Spark APIs."  Basically, Delta gives us the ability to create tables using Azure Databricks, with many of the fantastic features commonly found in proprietary database technologies such as:

• ACID Transactions: Delta guarantees that all readers and writers are working with consistent data, even in highly transactional environments.
• Scalable Metadata Handling: Delta improves on one of the most common issues with Data Lakes by managing metadata for billions of records at scale.
• Schema Enforcement: Delta can strongly enforce schema requirements for Delta-enabled tables.
• Time Travel: Delta can store historical data and automatically query relevant data for any requested time period.

In a future post, we'll take a look at each of these features, comparing Delta tables to traditional external hive tables.  Before that, we need a Data Frame and a couple tables to work with.  For these posts, we'll be working with Python and SQL because they are approachable and easy to code.

df

<CODE START>

df = sqlContext.read \
  .option("inferSchema", "true") \
  .csv("/databricks-datasets/adult/adult.data").toDF( \
    "age" \
    ,"workclass" \
    ,"fnlwgt" \
    ,"education" \
    ,"educationnum" \
    ,"maritalstatus" \
    ,"occupation" \
    ,"relationship" \
    ,"race" \
    ,"sex" \
    ,"capitalgain" \
    ,"capitalloss" \
    ,"hoursperweek" \
    ,"nativecountry" \
    ,"income" \
  )


df_adult.show(2)

<CODE END>

Next, let's create an external Hive table and a Delta table.

Save Hive Data

<CODE START>

df.write.format("parquet").mode("overwrite").save("/mnt/delta/hive/")

<CODE END>

Create Hive Table

<CODE START>

%sql

CREATE EXTERNAL TABLE hive (

  age INT

  ,workclass STRING

  ,fnlwgt DOUBLE

  ,education STRING

  ,educationnum DOUBLE

  ,maritalstatus STRING

  ,occupation STRING

  ,relationship STRING

  ,race STRING

  ,sex STRING

  ,capitalgain DOUBLE

  ,capitalloss DOUBLE

  ,hoursperweek DOUBLE

  ,nativecountry STRING

  ,income STRING

)

LOCATION '/mnt/delta/hive/'

STORED AS PARQUET

<CODE END>

Query Hive Table

<CODE START>

%sql

SELECT COUNT(1) FROM hive

<CODE END>

There's nothing new here.  For a more in-depth view of Hive tables, check out our earlier post on the topic.  Let's take a look at the Delta table now.

Save Delta Data

<CODE START>

df.write.format("delta").mode("overwrite").save("/mnt/delta/delta/")

<CODE END>

Create Delta Table

<CODE START>

%sql

CREATE TABLE delta

USING DELTA

LOCATION '/mnt/delta/delta/'

<CODE END>

Query Delta Table

<CODE START>

%sql

SELECT COUNT(1) FROM delta

<CODE END>

Saving the data in Delta format is as simple as replacing the .format("parquet") function with .format("delta").  However, we see a major difference when we look at the table creation.  When creating a table using Delta, we don't have to specify the schema, because the schema is already strongly defined when we save the data.  We also see that Delta tables can be easily queried using the same SQL we're used to.  Next, let's compare what the raw files look like by examining the blob storage container that we are storing them in.

Hive Files

Delta Files

The main difference we see is that the Delta files maintain a log, while the Hive files do not.  This is one of the major features that allows Delta tables to function more like mature database tables.  It also enables the Time Travel feature.  Let's use ParquetViewer to take a peak at these files.

Hive Parquet File

Delta Parquet File

Excusing the small picture size, these files are identical.  Let's see what happens if we duplicate the data in the tables.

Insert Hive Data

<CODE START>

%sql

INSERT INTO hive

SELECT * FROM hive

<CODE END>

<CODE START>

%sql


SELECT COUNT(1) FROM hive

<CODE END>

Insert Delta Data

<CODE START>

%sql

INSERT INTO delta

SELECT * FROM delta

<CODE END>

<CODE START>

%sql

SELECT COUNT(1) FROM delta

<CODE END>

We see that the INSERT commands ran perfectly for the Hive and Delta tables.  Let's see what the storage looks like now.

Duplicated Hive Files

Duplicated Delta Files

Duplicated Delta Logs

We see that the Hive files use the "_committed_", "_started_", and "_SUCCESS" files to log their changes, while the Delta files have a separate "_delta_log" folder with crc and json files.  Next, let's check out the differences between these files.

Hive _committed_

Despite not having a file extension, the Hive "_committed_" file is json formatted and only displays the files that were added and removed from the directory.  The other "_committed" file looks identical with a different file name in the "added" section.  Let's move on to the Delta log files.

Duplicated Delta Logs commitInfo

The "00000000000000000000.json" file was written when the table was originally created and populated.  It contains multiple sections, the first of which is the "commitInfo" section with basic information about the action that was taken.

Duplicated Delta Logs protocol

The "protocol" section appears to contain information about who can read or write either the table files or the log files.  Perhaps this will make more sense as we see more examples.

Duplicated Delta Logs metadata

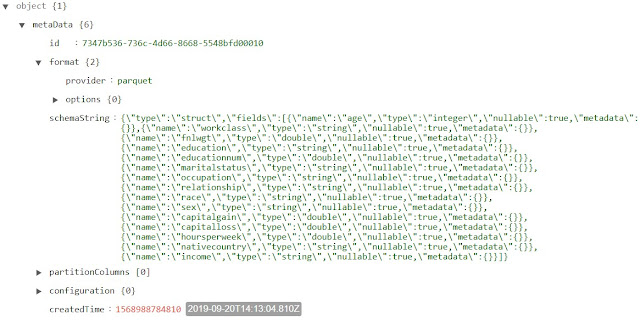
The "metadata" section contains all of the format and schema information about the table.  Interestingly, the "schemaString" attribute is an escaped JSON string.  Let's manually deconstruct it to see its format.

Duplicated Delta Logs schemaString

As expected, the "schemaString" attribute has a ton of information about each field, stored in an array named "fields".

Duplicated Delta Logs add

Moving on to the file section of the first file, we see that the "add" section has information on the file that was added.  This includes some basic stats about the data.  Let's unwrap this field as well.

Duplicated Delta Logs stats

The "stats" section contains the total number of records in the file, as well as the minimum, maximum and number of nulls in each field.  Now, let's take a look at the "00000000000000000001.json" file.

Duplicated Delta Logs commitInfo 2

Since this file was created by the duplication operation, it has its own "commitInfo" section that looks very similar to the previous one.  The major difference is that the "operationParameters.mode" attribute is Append instead of Overwrite.

Duplicated Delta Logs add 2

The "add" section looks virtually identical to the one we saw previously.  This makes sense because we did an exact duplication of the data in the table.

So, we've seen what happens when we add records to the table.  But, what happens when update or delete records, or even drop the entire table?  These questions will have to wait for later posts.  We hope that this post enlightened you a little bit to the purpose and structure of Azure Databricks Delta.  Stay tuned for the next post where we'll dig a little deeper into the inner workings.  Thanks for reading.  We hope you found this informative.

Brad Llewellyn
Service Engineer - FastTrack for Azure
Microsoft
@BreakingBI
www.linkedin.com/in/bradllewellyn
llewellyn.wb@gmail.com

Azure Databricks: RDDs, Data Frames and Datasets, Part 4

Today, we're going to continue talking about RDDs, Data Frames and Datasets in Azure Databricks.  If you haven't read the previous posts in this series, Introduction, Cluser Creation, Notebooks, Databricks File System (DBFS), Hive (SQL) Database and RDDs, Data Frames and Dataset (Part 1, Part 2, Part 3), they may provide some useful context.  If you are new to this material, it is especially important that you read through the previous posts (Part 1, Part 2, Part 3), as this post will build directly on what was discussed during the previous post.  You can find the files from this post in our GitHub Repository.  Let's move on to the core of this post, RDDs, Data Frames and Datasets.

Over the previous posts in this series (Part 1, Part 2, Part 3), we've written a number of code snippets that perform common data transformation tasks using RDDs, Data Frames and Datasets.  In this post, we're going to crank up the size of the data to see the performance differences between these methods.  Here's the code we used to create our new objects.

<CODE START>

for( i <- 1 to 1000){
  dbutils.fs.cp("/databricks-datasets/adult/adult.data", "/adultbig/adult" + i + ".data")
}

<CODE END>

<CODE START>

import org.apache.spark.sql.functions._

val rdd_lines = sc.textFile("/adultbig/")

val rdd_adult = rdd_lines
  .filter(f => f != "")
  .map(l => l.split(", "))

val df_adult_names = sqlContext.read
  .option("inferSchema", "true")
  .csv("/adultbig/").toDF(
    "age"
    ,"workclass"
    ,"fnlwgt"
    ,"education"
    ,"educationnum"
    ,"maritalstatus"
    ,"occupation"
    ,"relationship"
    ,"race"
    ,"sex"
    ,"capitalgain"
    ,"capitalloss"
    ,"hoursperweek"
    ,"nativecountry"
    ,"income"
  )

case class Adult (
  age: Int
  ,workclass: String
  ,fnlwgt: Double
  ,education: String
  ,educationnum: Double
  ,maritalstatus: String
  ,occupation: String
  ,relationship: String
  ,race: String
  ,sex: String
  ,capitalgain: Double
  ,capitalloss: Double
  ,hoursperweek: Double
  ,nativecountry: String
  ,income: String
)


val ds_adult = df_adult_names.as[Adult]

<CODE END>

Here's a copy of the code that we are running to test our objects.  Due to Spark's lazy evaluation framework, we have to use the .count function at the end of every command for force evaluation.  Since this is quite a few code segments, we'll use code blocks only to separate RDDs, Data Frames and Datasets, but break the individual code segments up by comment lines for clarity.

<CODE START>

rdd_adult.count

//

val rdd_select = rdd_adult
  .map(x => (x(0), x(14)))
rdd_select.count

//

val rdd_col = rdd_adult
  .map(x => (x(0), x(0).toInt * 12))
rdd_col.count

//

val rdd_fil = rdd_adult
  .filter(x => x(14) == "<=50K")
rdd_fil.count

//

val rdd_sum = rdd_adult
  .map(x => x(10).toDouble)
  .reduce((a, b) => a + b)
rdd_sum

//

val rdd_avg_tup = rdd_adult
  .map(x => x(0).toInt)
  .aggregate((0, 0))(
    (w, age) => (w._1 + age, w._2 + 1)
    ,(a, b) => (a._1 + b._1, a._2 + b._2)
  )
val rdd_avg = rdd_avg_tup._1.toDouble / rdd_avg_tup._2
rdd_avg

//

val rdd_aapi = rdd_adult
  .map(x => (x(14), x(0).toInt))
  .aggregateByKey((0, 0))(
    (w, age) => (w._1 + age, w._2 + 1)
    ,(a, b) => (a._1 + b._1, a._2 + b._2)
  )
  .map(x => (x._1, x._2._1.toDouble / x._2._2))
rdd_aapi.count

//

val rdd_lines_100 = sc.textFile("/adult100/")

val rdd_adult_100 = rdd_lines_100
  .filter(f => f != "")
  .map(l => l.split(", "))

val rdd_aapi_100 = rdd_adult_100
  .map(x => (x(14), x(0).toInt))
  .aggregateByKey((0, 0))(
    (w, age) => (w._1 + age, w._2 + 1)
    ,(a, b) => (a._1 + b._1, a._2 + b._2)
  )
  .map(x => (x._1, x._2._1.toDouble / x._2._2))

//

val rdd_join_l = rdd_adult_100
  .map(x => (x(14), x))

val rdd_join_r = rdd_aapi_100
  .map(x => (x._1, x))

val rdd_join = rdd_join_l
  .join(rdd_join_r)
  .map(x => (
    x._2._1(0)
    ,x._2._1(1)
    ,x._2._1(2)
    ,x._2._1(3)
    ,x._2._1(4)
    ,x._2._1(5)
    ,x._2._1(6)
    ,x._2._1(7)
    ,x._2._1(8)
    ,x._2._1(9)
    ,x._2._1(10)
    ,x._2._1(11)
    ,x._2._1(12)
    ,x._2._1(13)
    ,x._2._1(14)
    ,x._2._2._2
  ))
rdd_join.count

//

val rdd_sort = rdd_adult
  .sortBy(x => x(0))
rdd_sort.count

//

val rdd_sort2 = rdd_adult
  .sortBy(x => (x(0), x(1)))
rdd_sort2.count

<CODE END>

<CODE START>

df_adult_names.count

//

val df_select = df_adult_names
  .select("age", "income")
df_select.count

//

val df_col = df_adult_names
  .withColumn("ageinmonths", $"age" * 12)
  .select("age", "ageinmonths")
df_col.count

//

val df_fil = df_adult_names
  .filter(ltrim($"income") === "<=50K")
df_fil.count

//

val df_sum = df_adult_names
  .agg(sum("capitalgain"))
  .first()
  .getDouble(0)
df_sum

//

val df_avg = df_adult_names
  .agg(avg("age"))
  .first()
  .getDouble(0)
df_avg

//

val df_aapi = df_adult_names
  .groupBy("income")
  .agg(avg("age"))
df_aapi.count

//

val df_adult_100 = sqlContext.read
  .option("inferSchema", "true")
  .csv("/adult100/").toDF(
    "age"
    ,"workclass"
    ,"fnlwgt"
    ,"education"
    ,"educationnum"
    ,"maritalstatus"
    ,"occupation"
    ,"relationship"
    ,"race"
    ,"sex"
    ,"capitalgain"
    ,"capitalloss"
    ,"hoursperweek"
    ,"nativecountry"
    ,"income"
  )

val df_aapi_100 = df_adult_100
  .groupBy("income")
  .agg(avg("age"))

//

val df_join_r = df_aapi_100
  .withColumnRenamed("income", "rincome")

val df_join = df_adult_100
  .join(
    df_join_r
    ,df_adult_100("income") === df_join_r("rincome")
    ,"inner"
  )
  .drop("rincome")
df_join.count

//

val df_sort = df_adult_names
  .orderBy("age")
df_sort.count

//

val df_sort2 = df_adult_names
  .orderBy("age", "workclass")
df_sort2.count

<CODE END>

<CODE START>

ds_adult.count

//

case class Adult_select (
  age: Int
  ,income: String
)

val ds_select = ds_adult
  .select("age", "income")
  .as[Adult_select]
ds_select.count

//

case class Adult_col (
  age: Int
  ,ageinmonths: Int
)

val ds_col = ds_adult
  .withColumn("ageinmonths", $"age" * 12)
  .select("age", "ageinmonths")
  .as[Adult_col]
ds_col.count

//

val ds_fil = ds_adult
  .filter(ltrim($"income") === "<=50K")
ds_fil.count

//

val ds_sum = ds_adult
  .agg(sum("capitalgain"))
  .first()
  .getDouble(0)
ds_sum

//

val ds_avg = ds_adult
  .agg(avg("age"))
  .first()
  .getDouble(0)
ds_avg

//

case class Adult_aapi (
  income: String
  ,avgage: Double
)

val ds_aapi = ds_adult
  .groupBy("income")
  .agg(avg("age"))
  .withColumnRenamed("avg(age)", "avgage")
  .as[Adult_aapi]
ds_aapi.count

//

val ds_adult_100 = df_adult_100.as[Adult]

val ds_aapi_100 = ds_adult_100
  .groupBy("income")
  .agg(avg("age"))
  .withColumnRenamed("avg(age)", "avgage")
  .as[Adult_aapi]

//

case class Adult_join_r (
  rincome: String
  ,avgage: Double
)

val ds_join_r = ds_aapi_100
  .withColumnRenamed("income", "rincome")
  .as[Adult_join_r]

case class Adult_join (
  age: Int
  ,workclass: String
  ,fnlwgt: Double
  ,education: String
  ,educationnum: Double
  ,maritalstatus: String
  ,occupation: String
  ,relationship: String
  ,race: String
  ,sex: String
  ,capitalgain: Double
  ,capitalloss: Double
  ,hoursperweek: Double
  ,nativecountry: String
  ,income: String
  ,avgage: Double
)

val ds_join = ds_adult_100
  .join(
    ds_join_r
    ,ds_adult_100("income") === ds_join_r("rincome")
    ,"inner"
  )
  .drop("rincome")
  .as[Adult_join]
ds_join.count

//

val ds_sort = ds_adult
  .orderBy("age")
ds_sort.count

//

val ds_sort2 = ds_adult
  .orderBy("age", "workclass")
ds_sort2.count

<CODE END>

While performing this test, we found that the RDD join was continously failing due to memory errors.  While this was likely due to the fact that the RDDs were using strings, while the Data Frames and Datasets were using numeric types, we wanted to keep everything the same as we had seen previously.  So, we created a second set of objects that only used 10% of the total records to allow the RDD join to function.  Here are the results from the test.

Task	RDD	Data Frame	Dataset
Count	17.3	14.2	16.4
Select	16.4	13.4	13.8
New Column	16.8	13.7	12.9
Filtering	15.7	16.3	16.2
Sum	15.9	16.2	15.7
Average	16.4	37.4	16.5
Grouped Average	17.6	16.0	14.9
Join (10% of records)	27.8	5.6	5.1
Single Sort	91.2	32.6	30.2
Double Sort	95.4	32.6	34.8

Interestingly, we see that RDDs were rarely the more efficient option.  Even more surprisingly, Datasets were typically the most performant option and even when they weren't, they were very close.

So, it seems like we've found a nice trichotomy here.  RDDs are incredibly flexible and can perform virtually any analysis, but that comes at the cost of code complexity and (possibly) performance.  Data Frames can perform many of the analyses that we typically see in Data Engineering scenarios with the least code complexity and good performance.  Datasets perform slightly better than Data Frames with similar code, slightly bloated by the explicit casting.

We hope this mini-series on data objects was as education for you as it was for us.  This exercise has really opened our minds to what's possible in Azure Databricks.  Stay tuned for the next post, where we'll dig into Azure Databricks Delta Lake.  Thanks for reading.  We hope you found this informative.

Brad Llewellyn
Service Engineer - FastTrack for Azure
Microsoft
@BreakingBI
www.linkedin.com/in/bradllewellyn
llewellyn.wb@gmail.com

Azure Databricks: RDDs, Data Frames and Datasets, Part 3

Today, we're going to continue talking about RDDs, Data Frames and Datasets in Azure Databricks.  If you haven't read the previous posts in this series, Introduction, Cluser Creation, Notebooks, Databricks File System (DBFS), Hive (SQL) Database and RDDs, Data Frames and Dataset (Part 1, Part 2), they may provide some useful context.  If you are new to this material, it is especially important that you read through the previous posts (Part 1, Part 2), as this post will build directly on what was discussed during the previous post.  You can find the files from this post in our GitHub Repository.  Let's move on to the core of this post, RDDs, Data Frames and Datasets.

Before we begin, the following code block will create all of the necessary objects from the previous posts (Part 1, Part 2).

<CODE START>

import org.apache.spark.sql.functions._

val rdd_lines = sc.textFile("/databricks-datasets/adult/adult.data")

val rdd_adult = rdd_lines
  .filter(f => f != "")
  .map(l => l.split(", "))

val df_adult_nonames = sqlContext.read.csv("/databricks-datasets/adult/adult.data")

val df_adult_names = sqlContext.read
  .option("inferSchema", "true")
  .csv("/databricks-datasets/adult/adult.data").toDF(
    "age"
    ,"workclass"
    ,"fnlwgt"
    ,"education"
    ,"educationnum"
    ,"maritalstatus"
    ,"occupation"
    ,"relationship"
    ,"race"
    ,"sex"
    ,"capitalgain"
    ,"capitalloss"
    ,"hoursperweek"
    ,"nativecountry"
    ,"income"
  )

case class Adult (
  age: Int
  ,workclass: String
  ,fnlwgt: Double
  ,education: String
  ,educationnum: Double
  ,maritalstatus: String
  ,occupation: String
  ,relationship: String
  ,race: String
  ,sex: String
  ,capitalgain: Double
  ,capitalloss: Double
  ,hoursperweek: Double
  ,nativecountry: String
  ,income: String
)

val ds_adult = df_adult_names.as[Adult]

val rdd_select = rdd_adult
  .map(x => (x(0), x(14)))

val df_select = df_adult_names
  .select("age", "income")

case class Adult_select (
  age: Int
  ,income: String
)

val ds_select = ds_adult
  .select("age", "income")
  .as[Adult_select]

case class Adult_map (
  age: Int
  ,income: String
)

val ds_map = ds_adult
  .map(x => (x.age, x.income))
  .withColumnRenamed("_1", "age")
  .withColumnRenamed("_2", "income")
  .as[Adult_map]

val rdd_col = rdd_adult
  .map(x => (x(0), x(0).toInt * 12))

val df_col = df_adult_names
  .withColumn("ageinmonths", $"age" * 12)
  .select("age", "ageinmonths")

case class Adult_col (
  age: Int
  ,ageinmonths: Int
)

val ds_col = ds_adult
  .withColumn("ageinmonths", $"age" * 12)
  .select("age", "ageinmonths")
  .as[Adult_col]

val rdd_fil = rdd_adult
  .filter(x => x(14) == "<=50K")

val df_fil = df_adult_names
  .filter(ltrim($"income") === "<=50K")

val ds_fil = ds_adult
  .filter(ltrim($"income") === "<=50K")

val rdd_sum = rdd_adult
  .map(x => x(10).toDouble)
  .reduce((a, b) => a + b)

val df_sum = df_adult_names
  .agg(sum("capitalgain"))
  .first()
  .getDouble(0)

val ds_sum = ds_adult
  .agg(sum("capitalgain"))
  .first()
  .getDouble(0)

val rdd_avg_tup = rdd_adult
  .map(x => x(0).toInt)
  .aggregate((0, 0))(
    (w, age) => (w._1 + age, w._2 + 1)
    ,(a, b) => (a._1 + b._1, a._2 + b._2)
  )
val rdd_avg = rdd_avg_tup._1.toDouble / rdd_avg_tup._2

val df_avg = df_adult_names
  .agg(avg("age"))
  .first()
  .getDouble(0)

val ds_avg = ds_adult
  .agg(avg("age"))
  .first()
  .getDouble(0)

val ttuple = (1,2,3)
val tarray = Array(1,2,3)

val rdd_aapi = rdd_adult
  .map(x => (x(14), x(0).toInt))
  .aggregateByKey((0, 0))(
    (w, age) => (w._1 + age, w._2 + 1)
    ,(a, b) => (a._1 + b._1, a._2 + b._2)
  )
  .map(x => (x._1, x._2._1.toDouble / x._2._2))

val df_aapi = df_adult_names
  .groupBy("income")
  .agg(avg("age"))

case class Adult_aapi (
  income: String
  ,avgage: Double
)

val ds_aapi = ds_adult
  .groupBy("income")
  .agg(avg("age"))
  .withColumnRenamed("avg(age)", "avgage")
  .as[Adult_aapi]

<CODE END>

In the previous posts (Part 1, Part 2), we've looked at a number of basic transformations and aggregations.  Now, let's take a look at joining objects together.  In the previous post, we created objects containing the average age per income level.  Let's try joining those into the original objects.

Join RDD Code

Join RDD Output

<CODE START>

val rdd_join_l = rdd_adult
  .map(x => (x(14), x))

val rdd_join_r = rdd_aapi
  .map(x => (x._1, x))

val rdd_join = rdd_join_l
  .join(rdd_join_r)
  .map(x => (
    x._2._1(0)
    ,x._2._1(1)
    ,x._2._1(2)
    ,x._2._1(3)
    ,x._2._1(4)
    ,x._2._1(5)
    ,x._2._1(6)
    ,x._2._1(7)
    ,x._2._1(8)
    ,x._2._1(9)
    ,x._2._1(10)
    ,x._2._1(11)
    ,x._2._1(12)
    ,x._2._1(13)
    ,x._2._1(14)
    ,x._2._2._2
  ))

rdd_join.take(2)

<CODE END>

Join Data Frame

<CODE START>

val df_join_r = df_aapi
  .withColumnRenamed("income", "rincome")

val df_join = df_adult_names
  .join(
    df_join_r
    ,df_adult_names("income") === df_join_r("rincome")
    ,"inner"
  )
  .drop("rincome")

df_join.show(2)

<CODE END>

Join Dataset Code

Join Dataset Output

<CODE START>

case class Adult_join_r (
  rincome: String
  ,avgage: Double
)

val ds_join_r = ds_aapi
  .withColumnRenamed("income", "rincome")
  .as[Adult_join_r]

case class Adult_join (
  age: Int
  ,workclass: String
  ,fnlwgt: Double
  ,education: String
  ,educationnum: Double
  ,maritalstatus: String
  ,occupation: String
  ,relationship: String
  ,race: String
  ,sex: String
  ,capitalgain: Double
  ,capitalloss: Double
  ,hoursperweek: Double
  ,nativecountry: String
  ,income: String
  ,avgage: Double
)

val ds_join = ds_adult
  .join(
    ds_join_r
    ,ds_adult("income") === ds_join_r("rincome")
    ,"inner"
  )
  .drop("rincome")
  .as[Adult_join]

ds_join.show(2)

<CODE END>

We can make use of the built-in .join() function for RDDs.  Similar to the .aggregateByKey() function we saw in the previous post, the .join() function for RDDs requires a 2-element tuple, with the first element being the key and the second element being the value.  So, we need to use the .map() function to restructure our RDDs to store the keys in the first element and the original array/tuple in the second element.  After the join, we end up with an awkward nested structure of arrays and tuples that we need to restructure using another .map() function, leading to a lengthy code snippet.

Data Frames and Datasets can also make use their own .join() function, with the ability to define a binary join condition using the === notation we saw in the previous post.  Since Data Frames and Datasets have column names, we need to rename the key column in the right Data Frame or Dataset using the .withColumnRenamed() function to avoid duplicate column names.  After that, we can drop the right key using the .drop() function.  Once again, we see that the primary difference when working with Datasets is that we need to explicitly create a case class for each new Dataset we create.

In this case, we wanted to perform an inner join.  However, we can also perform other join types using the leftOuterJoin(), rightOuterJoin() and fullOuterJoin() functions for RDDs.  Data Frames and Datasets have a bit more flexibility on this front, allowing us to pass in the following join types as strings: inner, cross, outer, full, full_outer, left, left_outer, right, right_outer, left_semi, left_anti.

Next, let's try sorting our objects by age.

Sort RDD

<CODE START>

val rdd_sort = rdd_adult
  .sortBy(x => x(0))

rdd_sort.take(2)

<CODE END>

Sort Data Frame

<CODE START>

val df_sort = df_adult_names
  .orderBy("age")

df_sort.show(2)

<CODE END>

Sort Dataset

<CODE START>

val ds_sort = ds_adult
  .orderBy("age")

ds_sort.show(2)

<CODE END>

We were able to leverage the sortBy() function to sort the RDD.  All we needed to provide was an anonymous function that returns the values of interest.  The Data Frame and Dataset were similarly simple, using the .orderBy() function and a column name.  Since the structure of the Dataset didn't change, we didn't need create a new case class for it.

Although, sorting by age alone doesn't produce repeatable results, as age is not unique.  So, let's sort by age and workclass.

Sort RDD 2

<CODE START>

val rdd_sort2 = rdd_adult
  .sortBy(x => (x(0), x(1)))

rdd_sort.take(2)

<CODE END>

Sort Data Frame 2

<CODE START>

val df_sort2 = df_adult_names
  .orderBy("age", "workclass")

df_sort2.show(2)

<CODE END>

Sort Dataset 2

<CODE START>

val ds_sort2 = ds_adult
  .orderBy("age", "workclass")

ds_sort2.show(2)

<CODE END>

We see that this is equally simple.  For RDDs, we need to use a tuple instead of a single value.  For Data Frames and Datasets, we need to pass additional column into the orderBy() function.

That's all of the functionality that we wanted to cover in this mini-series comparing the data storage objects.  Using the tools that we've found over these three posts, the majority of data transformation problems are within our grasp.  We've seen that, for the most part, Data Frames and Datasets provide much simpler and more readable code because of their SQL-esque nature.  But, there's still one more topic we need to cover, Performance.  Stay tuned for the next post where we'll ramp up the data volume to see if there are any substantial performance impacts of using these objects.  Thanks for reading.  We hope you found this informative.

Brad Llewellyn
Service Engineer - FastTrack for Azure
Microsoft
@BreakingBI
www.linkedin.com/in/bradllewellyn
llewellyn.wb@gmail.com

Azure Databricks: RDDs, Data Frames and Datasets, Part 2

Today, we're going to continue talking about RDDs, Data Frames and Datasets in Azure Databricks.  If you haven't read the previous posts in this series, Introduction, Cluser Creation, Notebooks, Databricks File System (DBFS), Hive (SQL) Database and RDDs, Data Frames and Dataset (Part 1), they may provide some useful context.  If you are new to this material, it is especially important that you read through the previous post, as this post will build directly on what was discussed during the previous post.  You can find the files from this post in our GitHub Repository.  Let's move on to the core of this post, RDDs, Data Frames and Datasets.

Before we begin, the following code block will create all of the necessary objects from the previous post.

<CODE START>

val rdd_lines = sc.textFile("/databricks-datasets/adult/adult.data")

val rdd_adult = rdd_lines
  .filter(f => f != "")
  .map(l => l.split(", "))

val df_adult_nonames = sqlContext.read.csv("/databricks-datasets/adult/adult.data")

val df_adult_names = sqlContext.read
  .option("inferSchema", "true")
  .csv("/databricks-datasets/adult/adult.data").toDF(
    "age"
    ,"workclass"
    ,"fnlwgt"
    ,"education"
    ,"educationnum"
    ,"maritalstatus"
    ,"occupation"
    ,"relationship"
    ,"race"
    ,"sex"
    ,"capitalgain"
    ,"capitalloss"
    ,"hoursperweek"
    ,"nativecountry"
    ,"income"
  )

case class Adult (
  age: Int
  ,workclass: String
  ,fnlwgt: Double
  ,education: String
  ,educationnum: Double
  ,maritalstatus: String
  ,occupation: String
  ,relationship: String
  ,race: String
  ,sex: String
  ,capitalgain: Double
  ,capitalloss: Double
  ,hoursperweek: Double
  ,nativecountry: String
  ,income: String
)

val ds_adult = df_adult_names.as[Adult]

val rdd_select = rdd_adult
  .map(x => (x(0), x(14)))

val df_select = df_adult_names
  .select("age", "income")

case class Adult_select (
  age: Int
  ,income: String
)

val ds_select = ds_adult
  .select("age", "income")
  .as[Adult_select]

case class Adult_map (
  age: Int
  ,income: String
)

val ds_map = ds_adult
  .map(x => (x.age, x.income))
  .withColumnRenamed("_1", "age")
  .withColumnRenamed("_2", "income")
  .as[Adult_map]

val rdd_col = rdd_adult
  .map(x => (x(0), x(0).toInt * 12))

val df_col = df_adult_names
  .withColumn("ageinmonths", $"age" * 12)
  .select("age", "ageinmonths")

case class Adult_col (
  age: Int
  ,ageinmonths: Int
)

val ds_col = ds_adult
  .withColumn("ageinmonths", $"age" * 12)
  .select("age", "ageinmonths")

  .as[Adult_col]

<CODE END>

In the previous post, we looked at selecting and creating columns.  Now, let's take it one step further by filtering each object to only records with Income = "<=50k".

Filter RDD

<CODE START>

val rdd_fil = rdd_adult
  .filter(x => x(14) == "<=50K")

rdd_fil.count()

<CODE END>

Filter Data Frame

<CODE START>

import org.apache.spark.sql.functions._

val df_fil = df_adult_names

  .filter(ltrim($"income") === "<=50K")

df_fil.count()

<CODE END>

Filter Dataset

<CODE START>

import org.apache.spark.sql.functions._

val ds_fil = ds_adult

  .filter(ltrim($"income") === "<=50K")

df_fil.count()

<CODE END>

We see that there are some differences between filtering RDDs, Data Frames and Datasets.  The first major difference is the same one we keep seeing, RDDs reference by indices instead of column names.  There's also an interesting difference of using 2 ='s vs 3 ='s for equality operators. Simply put, "==" tries to directly equate two objects, whereas "===" tries to dynamically define what "equality" means.  In the case of filter(), it's typically used to determine whether the value in one column (income, in our case) is equal to the value of another column (string literal "<=50K", in our case).  In other words, if you want to compare values in one column to values in another column, "===" is the way to go.

Interestingly, there was another difference caused by the way we imported our data.  Since we custom-built our RDD parsing algorithm to use <COMMA><SPACE> as the delimiter, we don't need to trim our RDD values.  However, we used the built-in sqlContext.read.csv() function for the Data Frame and Dataset, which doesn't trim by default.  So, we used the ltrim() function to remove the leading whitespace.  This function can be imported from the org.apache.spark.sql.functions library.

As a nice added bonus, filter doesn't change the structure of the record.  So, we didn't need to create a new case class for the Dataset.  Data Frames and Datasets also have access to the where() function that is identical to filter().

Now that we've seen how easy it is to filter, let's try calculating the sum of the "capitalgain" column.

Sum RDD

<CODE START>

val rdd_sum = rdd_adult
  .map(x => x(10).toDouble)
  .reduce((t, c) => t + c)

rdd_sum

<CODE END>

Sum Data Frame

 <CODE START>

import org.apache.spark.sql.functions._

val df_sum = df_adult_names
  .agg(sum("capitalgain"))
  .first()
  .getDouble(0)

df_sum

<CODE END>

Sum Dataset

<CODE START>

import org.apache.spark.sql.functions._

val ds_sum = ds_adult
  .agg(sum("capitalgain"))
  .first()
  .getDouble(0)

ds_sum

<CODE END>

Here, we see another substantial difference between RDDs, Data Frames and Datasets.  RDDs make use the reduce() function.  Basically, we use the map() function to pass in only a single value for each element.  This is the capitalgain for each person.  Then, the reduce() function initializes two variables, a and b.  The reduce() function is going to "reduce" the capitalgains down into a single number.  However, it doesn't guarantee the order in which this happens.  So, a and b represent capitalgain values from the RDD and they will be added to each other until we arrive at a single, final number, the sum.  Since we can't control the order with which the values are reduced, the reduce() function requires our operation to be commutative and associative, which is the case for addition.

We see that Data Frames and Datasets make this substantially easier via the use of the agg() function.  This function allows us to define aggregations against Data Frames or Datasets.  The complete list of aggregations that can be passed into the agg() function can be found here.  The agg() function outputs a 1-by-1 Data Frame, meaning that we need to retrieve the value using the first() and getDouble() functions.

Next, let's move on to a more complex aggregation, average age.

Average RDD

<CODE START>

val rdd_avg_tup = rdd_adult
  .map(x => x(0).toInt)
  .aggregate((0, 0))(
    (w, age) => (w._1 + age, w._2 + 1)
    ,(a, b) => (a._1 + b._1, a._2 + b._2)
  )
val rdd_avg = rdd_avg_tup._1.toDouble / rdd_avg_tup._2

rdd_avg

<CODE END>

Average Data Frame

<CODE START>

import org.apache.spark.sql.functions._

val df_avg = df_adult_names
  .agg(avg("age"))
  .first()
  .getDouble(0)

df_avg

<CODE END>

Average Dataset

<CODE START>

import org.apache.spark.sql.functions._

val ds_avg = ds_adult
  .agg(avg("age"))
  .first()
  .getDouble(0)

ds_avg

<CODE END>

We see the complexity of RDD operations ramping up even further.  The reduce() function is fantastic for performing a single, basic operation that is commutative and associative.  "Average" does not fall in this category.  Instead, it's a non-commutative, non-associative combination (division, quotient) of two commutative, associative operations, sum and count.  So, we need to use the more complex and flexible aggregate() function.

The first part of the aggregate function is the "zero value", i.e. the "starting value" for the aggregation.  In our case, we use the tuple (0, 0) to store the starting sum and starting count.  Then, we need to define the "within-partition" calculation.

This calculation will take in two variables, w and age.  It pulls "w", the starting value, from the first part of the aggregate() function and it pulls "age" from the RDD passed in by the previous map() function.  Using "w" and "age", it creates a tuple for each partition in the RDD.  The first element of the tuple is the sum, calculating by adding all of the "age" values, and the second element is the count, calculating by adding 1 for each "age" value.

Once the (sum, count) tuple is calculated for each partition, the final calculation functions identically to the way that reduce() does.  It pulls the (sum, count) tuples from the previous step and combines them together in whatever order it feels like.  To turn a set of sums and counts into an overall sum and and an overall count, all we need to do is add all of the sums together and add all the counts together.

Finally, we calculate the average by dividing the overall sum by the overall count.  We also have to cast the sum to a double beforehand because, as is true in many programming languages, Int / Int = Int in Scala, which would give us an answer of 38, instead of 38.581...

To add even more complexity, the syntax for pulling elements out of a Tuple is tuple._1, where index starts at 1, and the syntax for pulling elements out of an Array is array(index), where index starts at 0.

Tuple

<CODE START>

val ttuple = (1,2,3)

ttuple._1

<CODE END>

Array

<CODE START>

val tarray = Array(1,2,3)

tarray(0)

<CODE END>

On a completely separate, but similarly complex topic, we also haven't discussed partitions at this point.  Simply put, Spark is a distributed processing framework and many objects that we use are split across partitions to allow for parallel processing.  RDDs, Data Frames and Datasets are some of these objects.  Managing partitions is a more advanced topic that we may discuss in a later post.

Moving on, we see that Data Frames and Datasets make this operation much easier by providing a built-in avg() function.  For our final transformation in this post, let's calculate average age per income level.

Average Age by Income RDD

<CODE START>

val rdd_aapi = rdd_adult
  .map(x => (x(14), x(0).toInt))
  .aggregateByKey((0, 0))(
    (w, age) => (w._1 + age, w._2 + 1)
    ,(a, b) => (a._1 + b._1, a._2 + b._2)
  )
  .map(x => (x._1, x._2._1.toDouble / x._2._2))

rdd_aapi.collect()

<CODE END>

Average Age by Income Data Frame

<CODE START>

import org.apache.spark.sql.functions._

val df_aapi = df_adult_names
  .groupBy("income")
  .agg(avg("age"))

df_aapi.show()

<CODE END>

Average Age by Income Dataset

<CODE START>

import org.apache.spark.sql.functions._

case class Adult_aapi (
  income: String
  ,avgage: Double
)

val ds_aapi = ds_adult
  .groupBy("income")
  .agg(avg("age"))
  .withColumnRenamed("avg(age)", "avgage")
  .as[Adult_aapi]

ds_aapi.show()

<CODE END>

The RDD code is almost identical to the previous example.  However, there are a couple of differences.  First, we are creating a 2-element tuple in the first map() function, with the first element being the key, "income" in this case, and the second element being the value, "age" in this case.  Then, we use the aggregateByKey() function to perform the exact same aggregations as before.  This time however, it will aggregate the values by implicitly pulling them from the second element of the tuples passed in from the previous map() function.  It's important to note that we don't assign keys or values at any point here.  They are assumed to the be the first and second elements of the tuples, respectively.

Next, since this aggregateByKey() function is assumed to output more than one element, it passes an RDD instead of a tuple.  So, we can perform our final division by using another map() function, returning the income and average age values as an RDD of tuples.

Again, the Data Frame and Dataset code is drastically simpler, relying heavily on the groupBy() and agg() functions to do the heavy lifting.  Also, since we are now dealing with more than one record, we have to explicitly cast our Dataset again.  This also requires a column rename because parenthesis are not allowed in Dataset column names.

Hopefully this post shed a little more light on the data transformation methods in Azure Databricks.  We're starting to notice a trend of RDD operations being much complex than their Data Frame and Dataset counterparts.  Does this trend continue with other types of transformations?  Does it buy us any potential performance improvements?  Stay tuned for the next post where we'll dig even deeper into these questions.  Thanks for reading.  We hope you found this informative.

Brad Llewellyn
Service Engineer - FastTrack for Azure
Microsoft
@BreakingBI
www.linkedin.com/in/bradllewellyn
llewellyn.wb@gmail.com